不规则三角网TIN及其建立方法

不规则三角网（Triangulated Irregular Network，TIN）是另外一种表示数字高程模型的方法，是由Peuker和他的同事在1978年设计的一个系统，它是由不规则分布的离散数据点结构造出邻接的三角形（三角面）而组成的格网结构。

TIN模型根据区域有限个点集将区域划分为相连的三角面网络，区域内任意点落在三角面的顶点、边上或三角形内。如果点不在顶点上，该点的高程值通常通过线性插值的方法得到（在边上用边的两个顶点的高程，在三角形内则用三个顶点的高程）。所以TIN是一个三维空间的分段线性模型，在整个区域内连续但不可微。

不规则三角网数字高程由连续的三角面组成，三角面的形状和大小取决于不规则分布的测点或节点的位置和密度。

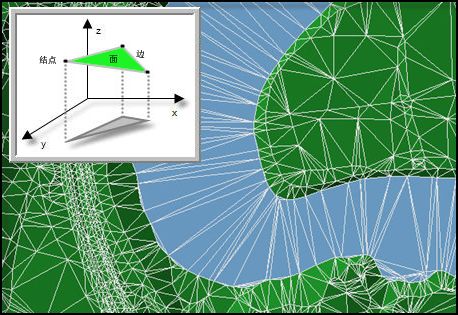
TIN表示法利用所有采样点取得的离散数据，按照优化组合的原则，把这些离散点（个三角形的顶点）连接成相互连续的三角面（在连接时，尽可能地确保每个三角形都是锐角三角形或是三边的长度近似相等）。

TIN是不规则网格中最简单的形态，在等高线追踪、三维显示及其他方面也是最常用、最简单的结构。

三角化算法分类：

1.不规则分布采样数据

• DT三角剖面

1. 直接DT（分割合并算法、逐点插入算法、空外接圆算法、三角形增长算法）；
2. 间接DT

• 规则分布采样数据

1. VIPs算法
2. 循环迭代算法
3. 层次三角形算法

• 沿等高线分布数据

1. 特征线法
2. 探测优化法

基于TIN建立的DEM的特点

• TIN能随地形起伏的复杂性而灵活地改变采样点的密度和确定离散采样点的位置因而它克服了因地形起伏不大而产生的高程矩阵中冗余数据的问题；
• 能按地形特征点和线，如山脊线、沟谷线、地形变换线和其它按精度要求进行数字化的重要地形特征来获取DEM数据，不改变原始数据及其精度，保持原有的关键地形特征；
• 能较好地处理不规则形状的区域边界；
• 有足够离散点的情况下效果好。

格网DEM与TIN、DEM的相互转换

格网DEM转成TIN

• 保留重点法
• 启发丢弃法

TIN转成格网DEM

• 将TIN看作普通的不规则数据点生成规则格网DEM；
• 将规则格网覆盖在TIN上，计算每个格网点落在哪个TIN三角形内，根据该三角面格顶点的高程进行线性内插，得到格网点的高程。